Shopping Cart

No products in the cart.

Shopping Cart

No products in the cart.

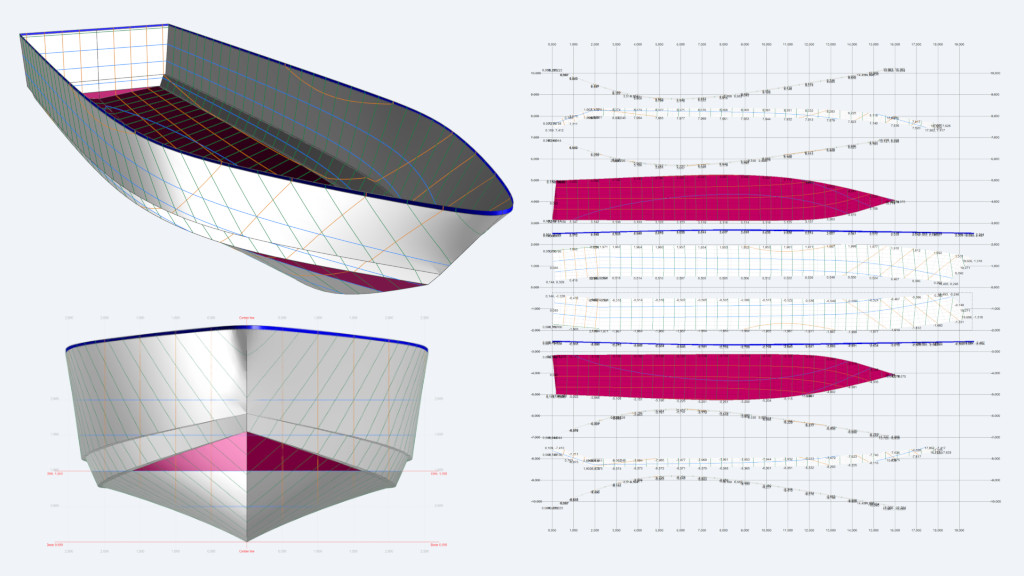
The meaning of circulation

Topics: Aero - Hydro | Aerodynamics | Hydrodynamics | Pablo Sopelana | Pro
Tagged:
Pablo Sopelana
470 International Class

Circulation is one of the most misunderstood terms in sailing. Yet, circulation is essential to understand lift and why sails, wingsails, keels, rudders, foils, etc., work. We can safely say that sailing is possible, at least when beating windward, thanks to circulation.

This content is for Pro (monthly) and Pro (annual) members only.
Upgrade
Already a member? Log in here
Topics: Aero - Hydro, Aerodynamics, Hydrodynamics, Pablo Sopelana, Pro
Tags:

Related

Courses

Go to Courses

Merch

Go to Merch

Send us a Message

    Report

    Harassment or bullying behavior
    Contains mature or sensitive content
    Contains misleading or false information
    Contains abusive or derogatory content
    Contains spam, fake content or potential malware

    Block Member?

    Please confirm you want to block this member.

    You will no longer be able to:

    • See blocked member's posts
    • Mention this member in posts
    • Invite this member to groups
    • Message this member
    • Add this member as a connection

    Please note: This action will also remove this member from your connections and send a report to the site admin. Please allow a few minutes for this process to complete.

    Report

    You have already reported this .