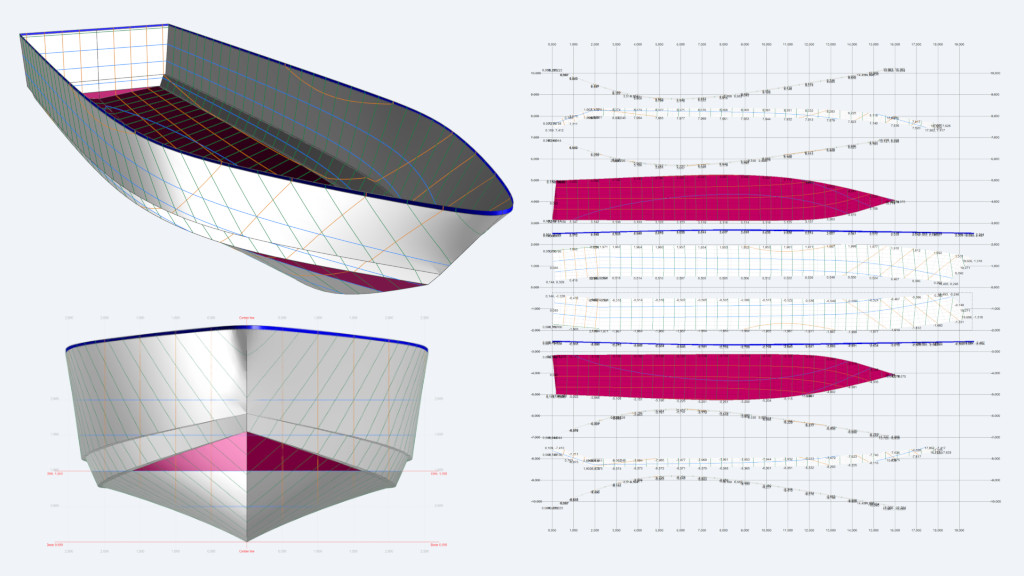
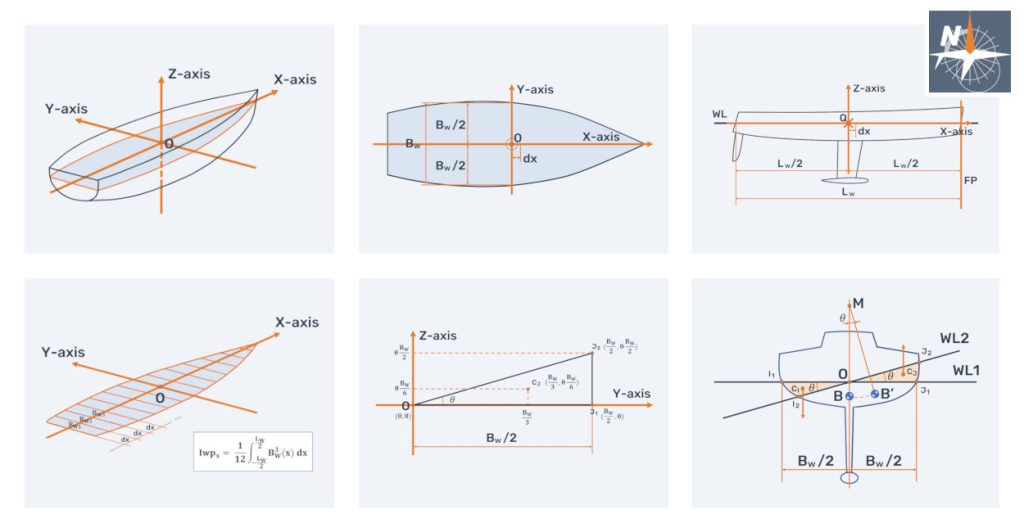
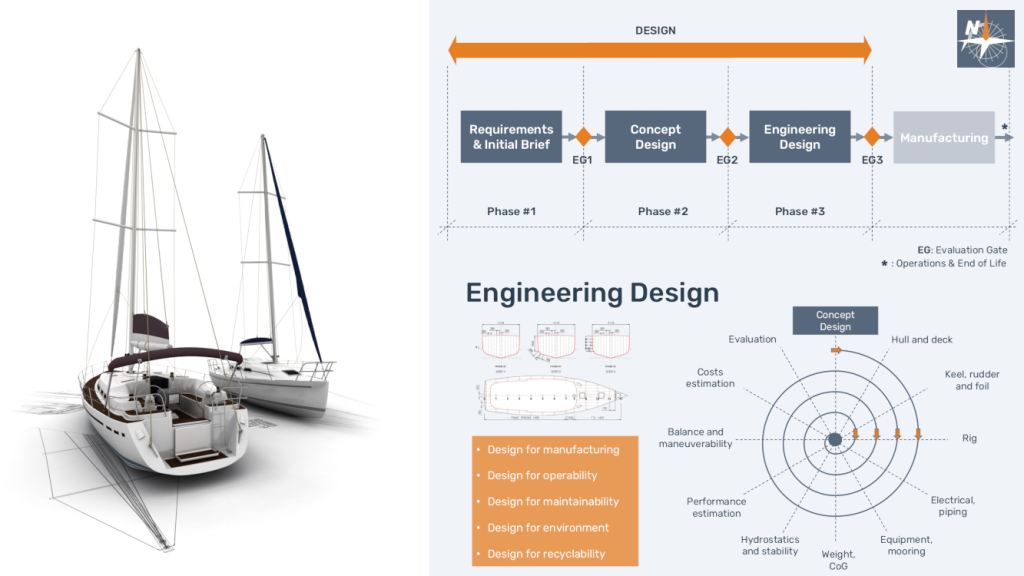
The Reynolds number
The Reynolds number is the ratio of inertia forces to viscous forces involved in the flow. Reynolds understood that while inertia forces were dominant in a turbulent flow, viscous forces were prevalent in a laminar one. In this way, the Reynolds number can be used to determine whether a flow is laminar or turbulent.
Already a member? Log in here
