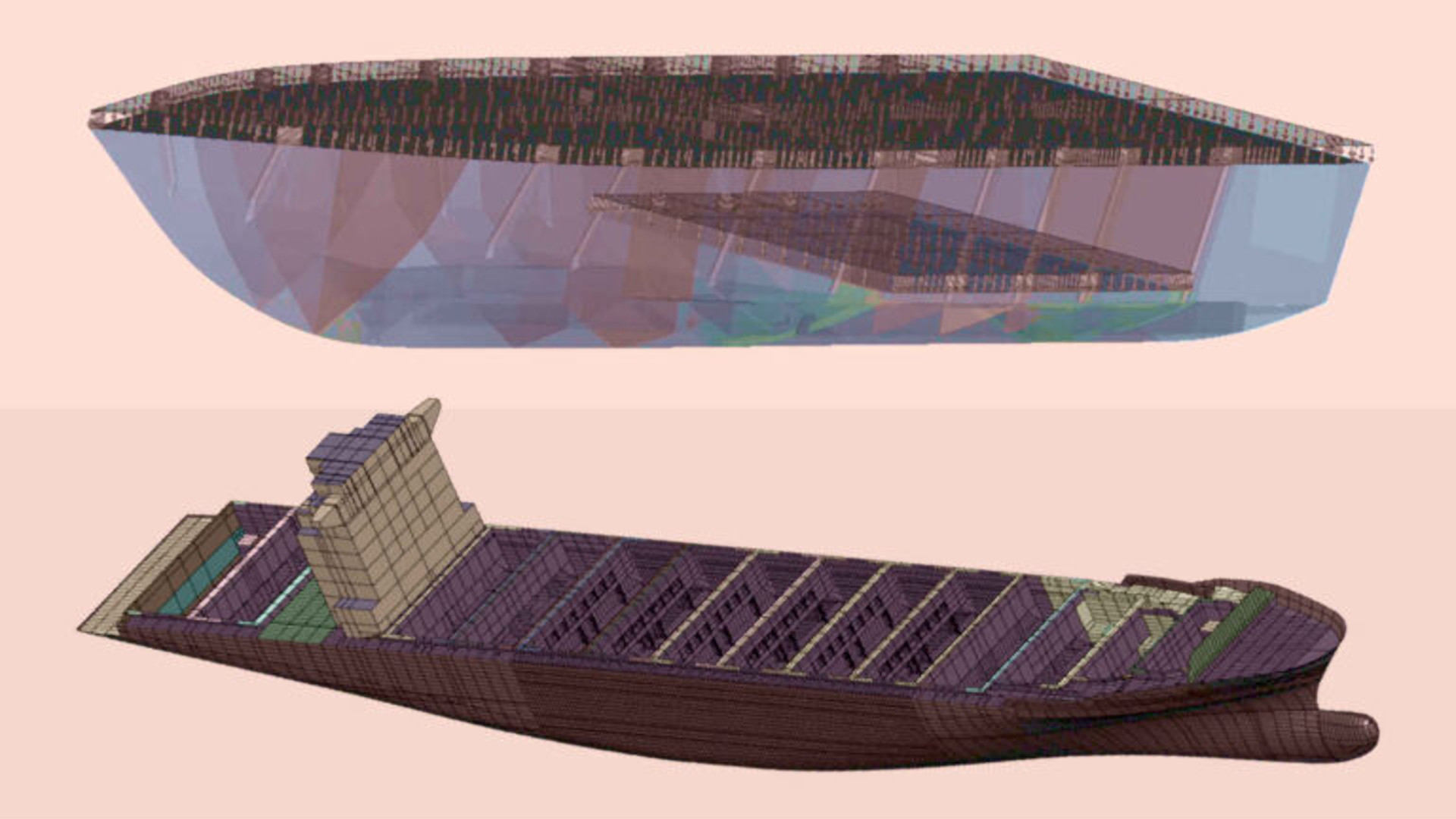
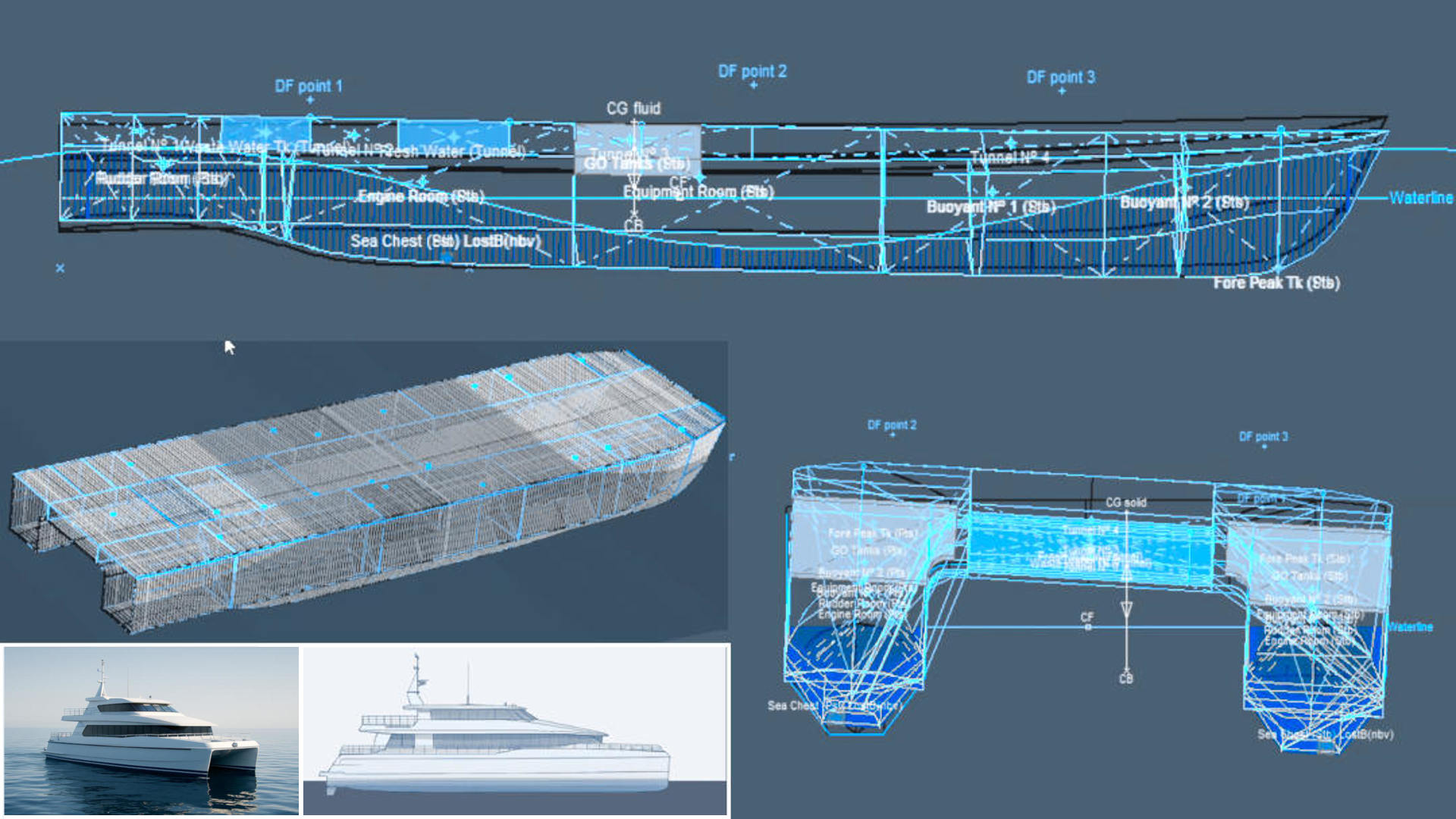
Navalapp
Yacht Design, Naval Architecture, and Ocean Engineering
Yacht Design, Naval Architecture, and Ocean Engineering
app
Dare Greatly. Live Boldly. Do It with Purpose.
We are on a journey to make Yacht Design, Naval Architecture, and Ocean Engineering accessible, advance the Marine Industry, and inspire a new generation of professionals.
Courses
Learn with video-based, self-paced, online courses with interactive quizzes, and downloadable resources.
Learning Paths
Develop foundational and advanced skills in a chosen area of expertise.
Assignments
Engage in exciting projects and received personalized feedback from the instructors.
Classrooms
Participate in class discussions with the instructors and fellow students.
Instructors
Learn from Professionals with a proven industry, research, and/or university record.
Resources
Gain access to articles, templates, software, books, and papers.
Campus
Connect with fellow students and share your journey with others.
Certificates
Make your knowledge count with Courses, Learning Paths, and Complete Program Certificates.
Career Development & Entrepreneurship
Introduce yourself and look for partners, cofounders, internships, and jobs.
Learning Paths
A Learning Path is a series of courses designed to guide you in a specific subject area. It provides a roadmap for you to follow and builds both foundational and advanced skills.
Design & Evaluation
This path provides a strong foundation in both the theoretical and practical aspects of yacht design, stability evaluation, software tools, and regulatory compliance. You will gain the skills to design yachts that are not only functional, but also safe and compliant with international standards.
Materials & Structures
Together, these courses will provide you with a robust understanding of both the structural design principles and the materials used in yacht construction. You will be equipped to make well-informed decisions about material selection and structural integrity, ensuring that your designs are compliant with industry standards.
Aero - Hydrodynamics
With this path, you will thoroughly understand fluid dynamics and its application to yacht design and performance analysis. You will also become proficient in utilizing software tools for conducting Computational Fluid Dynamics (CFD) simulations, enabling you to analyze and optimize performance.
Sail Design & Sailmaking
This path will equip you with a comprehensive knowledge in sail design and sailmaking, incorporating both theoretical understanding and practical skills. You will be prepared to design and manufacture sails and sail components with a strong grasp of both aerodynamic and material considerations.
Modeling & Rendering
This learning path is designed to provide you with advanced 3D modeling and rendering skills using industry-standard software. It covers fundamental to advanced techniques, and you will work on several projects.
Rules & Regulations
This path focuses on standards, rules, and regulations required for designing, evaluating, and certifying yachts. It ensures you gain a deep understanding and the ability to apply these requirements effectively in your projects.
Coding & AI & Machine Learning
This learning path equips you with a robust toolkit for leveraging data science and machine learning in the marine industry. You will start with fundamental programming skills and progressively tackle more complex data manipulation, visualization, and machine-learning techniques.
Offshore
The Offshore specialization is designed for professionals and enthusiasts seeking to deepen their knowledge in areas such as offshore wind energy, offshore oil and gas, marine renewables, and subsea infrastructure.
What are our Students saying?
Around the world
More than
Students
From more than
Countries
- The instructors are well prepared. 97%
- The courses met my expectations in terms of learning. 92%
- I am confident in applying what I learned. 96%
- The courses are helpful in progressing toward my goals. 93%
- I would recommend the course I have just finished. 95%
- I want to take more Navalapp courses. 97%
Latest Courses
Video-based, self-paced, and on-demand courses. They feature interactive quizzes and downloadable resources and give access to the course’s classroom, a virtual place where students can interact with the instructors and fellow students.
What do we do?
We help professionals, amateurs, and aspiring Yacht Designers, Naval Architects, and Ocean Engineers develop relevant skills, career advancement, unlock job opportunities, and transform their dreams into reality.
We create quality, authoritative and expert online courses, articles, calculation templates, and videos, related to Yacht Design, Naval Architecture, and Ocean Engineering.
We are on a journey to make Yacht Design, Naval Architecture, and Ocean Engineering accessible, providing quality education and learning opportunities for all.